On/Off-policy
- On-policy
- 學習的 agent 和與環境互動的 agent 是同一個
- Off-policy
- 學習的 agent 和與環境互動的 agent 是不同個
想從 On-policy 轉 Off-policy
- On-policy 每次都要重新蒐集資料,很花時間
- 由另一個 $\pi_{\theta^{'}}$ 去 train $\theta$,$\theta^{'}$是固定的,所以我們可以 re-use sample data
Importance Sampling
-
是一個 general 的想法,不限於 RL
-
$E_{x \text{\textasciitilde} p}[f(x)]\approx \frac{1}{N}\displaystyle\sum_{i=1}^N f(x^i)$
- $x^i$ is sampled from p(x)
-
我們遇到的問題是沒辦法從 p 來 sample data,只能透過 q(x) 去 sample $x^i$
-
可以把上式改寫成 $E_{x \text{\textasciitilde} p}[f(x)]=E_{x \text{\textasciitilde} q}[f(x)\frac{p(x)}{q(x)}]$
Issue
-
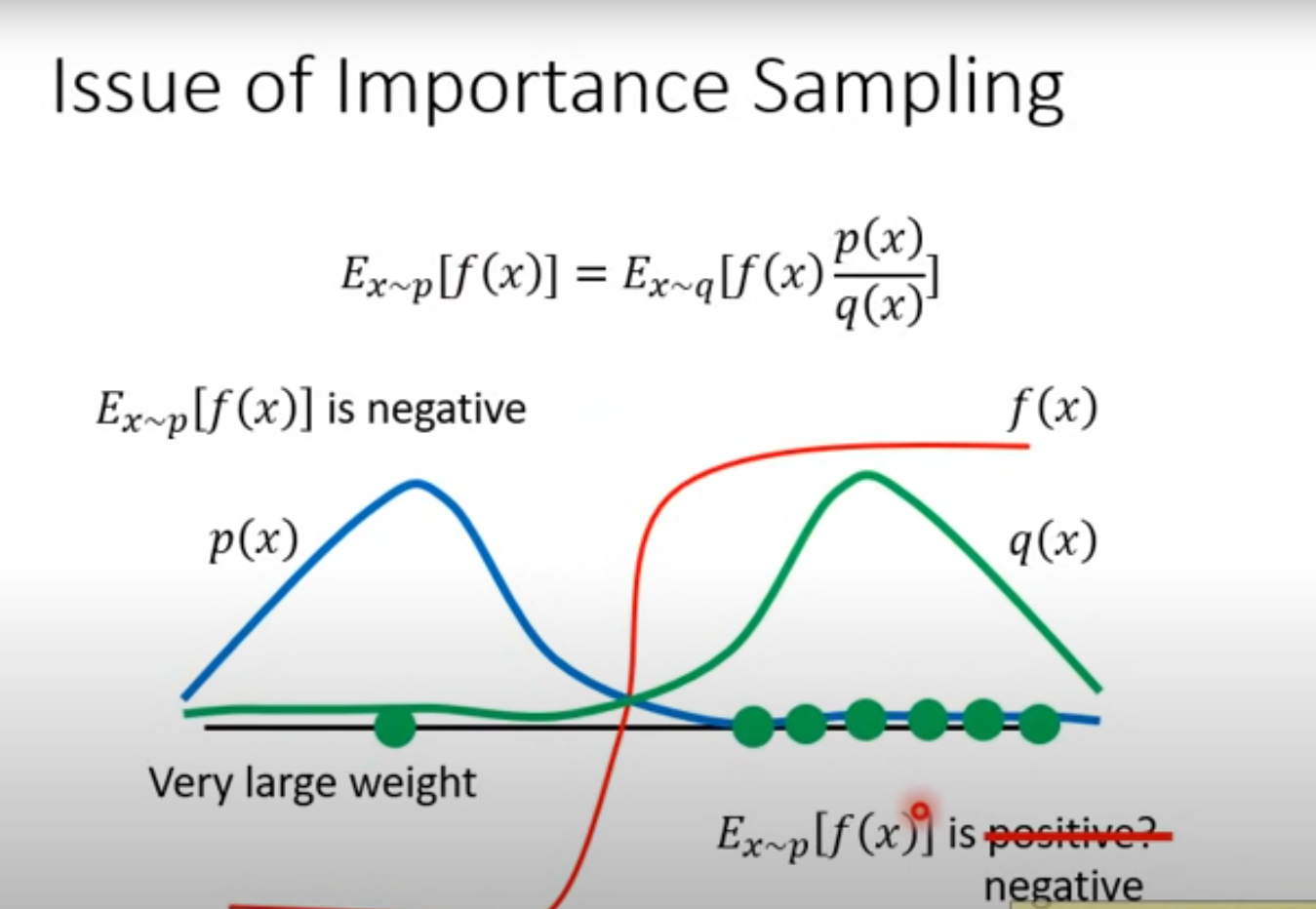
雖然理論上 q 可以任意選,只要不要 q(x) 是 0 的時候 p(x) 不是 0,實作上 p 和 q 不能差太多,不然會有問題
- 這兩項的 Variance 不一樣,如果 p 除以 q 差距很大,右邊的 Variance 會很大,如果 sample 不夠多次就會有問題
轉換
-
原本
- $\triangledown \overline{R_{\theta}}=E_{\tau \text{\textasciitilde}p_{\theta}(\tau)}[R(\tau)\triangledown log p_{\theta} (\tau)]$
-
改為
- $\triangledown \overline{R_{\theta}}=E_{\tau \text{\textasciitilde}p_{\theta^{'}}(\tau)}[\frac{p_{\theta}(\tau)}{p_{\theta^{'}}(\tau)}R(\tau)\triangledown log p_{\theta} (\tau)]$
- 從 $\theta^{'}$ sample 資料
- 更新 $\theta$ 多次
Advantage function
-
原本
- $E_{(s_t,a_t)\text{\textasciitilde}\pi_{\theta}}[A^{\theta}(s_t,a_t)\triangledown log p_\theta(a_t^n|s_t^n)]$
-
改為
- $E_{(s_t,a_t)\text{\textasciitilde}\pi_{\theta^{'}}}[\frac{P_\theta(s_t,a_t)}{P_{\theta^{'}}(s_t,a_t)}A^{\theta^{'}}(s_t,a_t)\triangledown log p_\theta(a_t^n|s_t^n)]$
- 要注意 Advantage 的結果要由 $\theta^{'}$ 得出,是 $\theta^{'}$在和環境互動
-
新的 objective function
- $J^{\theta^{'}}(\theta)=E_{(s_t,a_t)\text{\textasciitilde}\pi_{\theta^{'}}}[\frac{p_\theta(a_t|s_t)}{p_{\theta^{'}}(a_t|s_t)}A^{\theta^{'}}(s_t,a_t)]$
PPO
- 確保 $\theta$ 和 $\theta^{'}$ 不會差太多
- $J_{PPO}^{\theta^{'}}(\theta)=J^{\theta^{'}}(\theta)-\beta KL(\theta, \theta^{'})$
前身 TRPO
- Trust Region Policy Optimization
- $J_{TRPO}^{\theta^{'}}(\theta)=E_{(s_t,a_t)\text{\textasciitilde}\pi_{\theta^{'}}}[\frac{p_\theta(a_t|s_t)}{p_{\theta^{'}}(a_t|s_t)}A^{\theta^{'}}(s_t,a_t)], KL(\theta, \theta^{'})<\delta$
- constrain 很難處理
KL divergence
- 這邊不是 $\theta$ 和 $\theta^{'}$ 參數上的距離,而是 behavior 的距離
- 參數上的距離是指這兩個參數有多像
- 是給同樣的 state 生出 action 的 distribution 要像
algorithm
- 初始參數 $\theta^0$
- 每個 iteration
-
用 $\theta^k$ 和環境互動,蒐集{$s_t,a_t$},並計算 advantage $A^{\theta^k}(s_t,a_t)$
-
找出 theta 最佳化 $J_{PPO}(\theta)$
- $J_{PPO}^{\theta^{k}}(\theta)=J^{\theta^{k}}(\theta)-\beta KL(\theta, \theta^{k})$
- 可以更新很多次
-
動態調整 $\beta$
- Adaptive KL Penalty
- 設可接受的 KL 數值範圍
- if $KL(\theta,\theta^k)>KL_{max},\text{increase} \beta$
- if $KL(\theta,\theta^k)<KL_{min},\text{decrease} \beta$
-
PPO2
-
PPO
- $J_{PPO}^{\theta^{k}}(\theta)=J^{\theta^{k}}(\theta)-\beta KL(\theta, \theta^{k})$
-
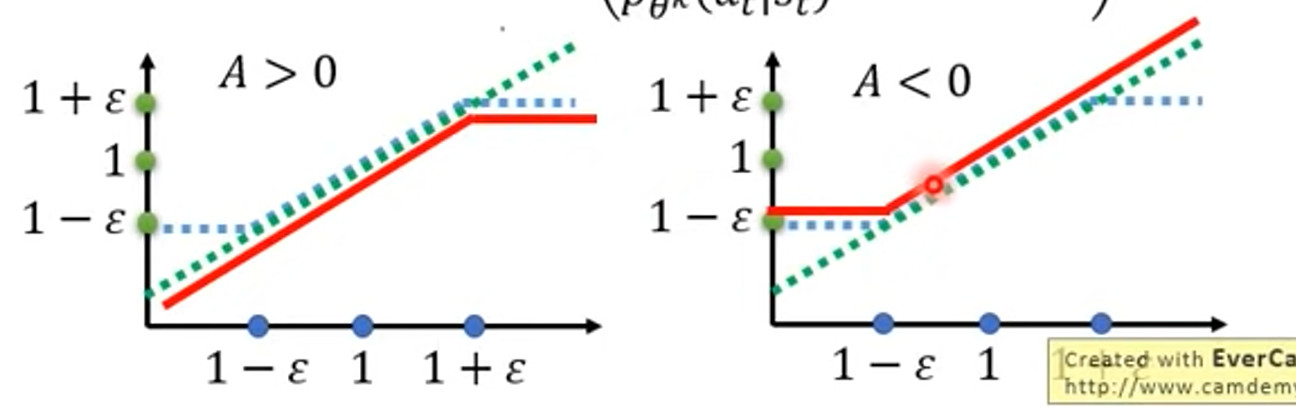
PPO2
- $J_{PPO2}^{\theta^{k}}(\theta)\approx \displaystyle\sum_{(s_t,a_t)}min(\frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}A^{\theta^k}(s_t,a_t), \\ clip(\frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}, 1-\varepsilon, 1+\varepsilon)A^{\theta^k}(s_t,a_t))$