Basic Components

  • Actor
    • Policy $\pi$ is a network with parameter $\theta$
  • Env
  • Reward Function

Trajectory

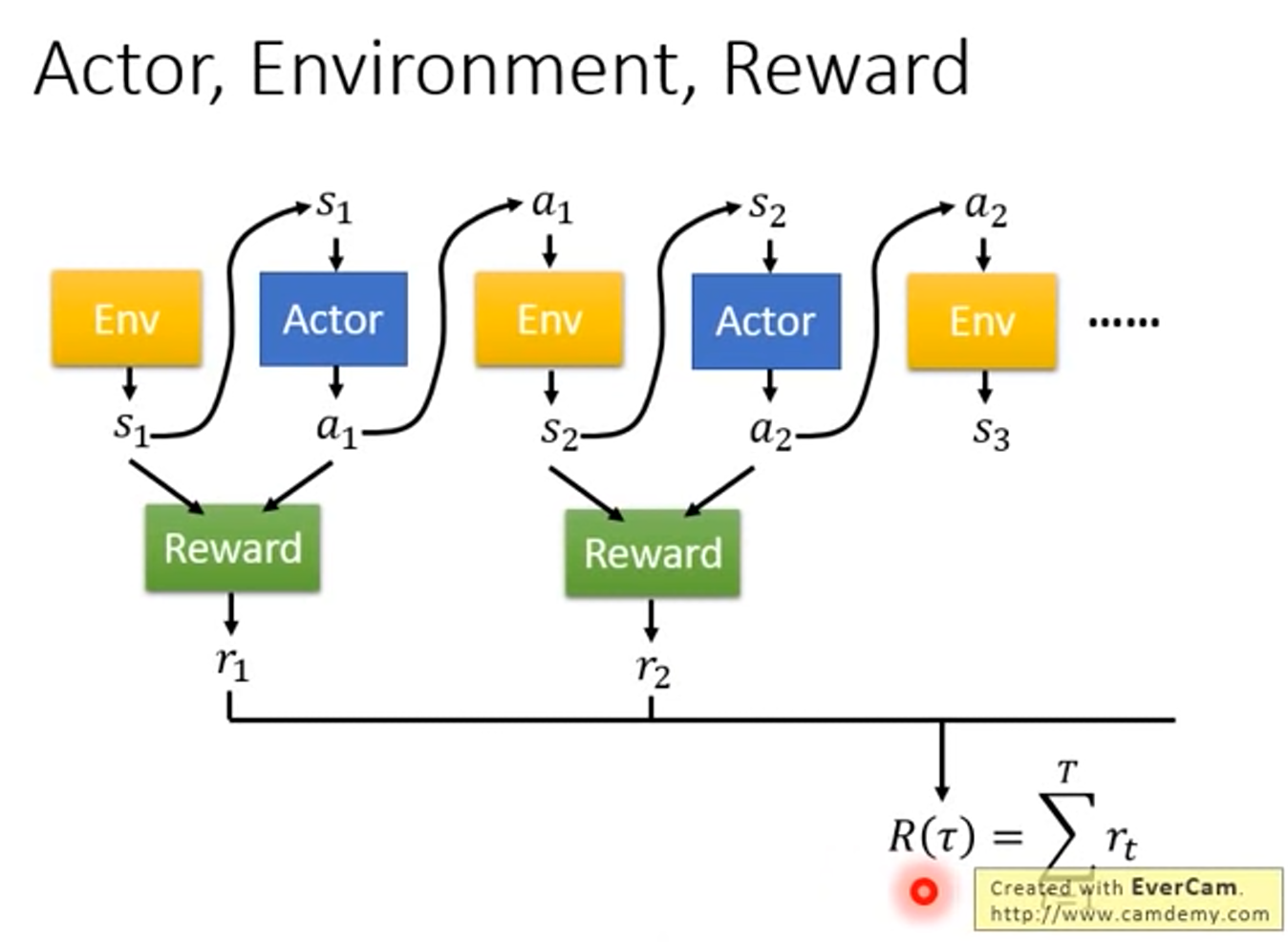
  • 在一場遊戲，把 env 輸出的 s 和 actor 輸出的 a 串起來，是一個 Trajectory
  • Trajectory $\tau$ = {$s_1,a_1,s_2,a_2,…,s_T,a_T$}
  • $p_{\theta}(\tau)=p(s_1)\displaystyle\prod_{t=1}^Tp_{\theta}(a_t|s_t)p(s_{t+1}|s_t,a_t)$

Update

$\theta \leftarrow \theta + \eta \triangledown \overline{R}_{\theta}$

$\triangledown \overline{R_{\theta}} = \displaystyle\sum_{\tau} R(\tau) \triangledown p_{\theta} (\tau) \\ =\frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{t=1}^{T_n}R(\tau^n)\triangledown log p_{\theta} (a_t^n|s_t^n)$

實作

  • 常見公式
    • $\triangledown f(x)=f(x)\triangledown logf(x)$
  1. 用當前模型蒐集一堆 Trajectory
  2. 更新模型
  3. 回到第一步
  • 細節
    • 做一個分類問題，把 state 當作分類器的 Input，把 action 當作分類器的 ground truth 作訓練
    • 在實作分類問題的時候，objective function 都會寫成 minimize cross entropy，就是 maximize log likelihood
    • RL 和一般分類的區別是，要記得在 loss 前面乘上 $R(\tau^n)$

Tip

  1. Add a Baseline
    • $R(\tau^n)$ 有可能永遠都為正
      • 此時等於告訴 Model 說，今天不管是什麼 action，都要提高它的機率。不一定會有問題，因為雖然都是正的，但正的量有大有小，可能某些 action 上升的幅度會更大。因為我們是在做 sampling，不一定會 sample 到某些 action，本來想的情況是所有的 trajectory 都會出現才沒問題。
    • 解法: 希望 reward 不要總是正的
      • $\triangledown \overline{R_{\theta}}\approx \frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{t=1}^{T_n}(R(\tau^n)-b)\triangledown log p_{\theta}(a_t^n|s_t^n)$
      • $b \approx E[R(\tau)]$
  2. Assign Suitable Credit
    • 原本整場遊戲的所有 action 都會乘上 $R(\tau)$，但這不太公平，因為就算結果是好的，不代表所有 action 都是對的，反之亦然。在理想的情況下，如果 sample 夠多，就可以解決這問題。
    • 解法
      1. 只計算從這個 action 後的 reward 總和
        • 因為前面的 reward 和你做了什麼沒關係
      2. 接續解法 1，把比較未來的 reward 做 discount
        • 乘某個小於 1 的 $\gamma^{t^{'}-t}$

Advantage function

  • base 可以是 state-dependent，可以根據 network 得出，以後再說
  • $(Reward-b)$ 可以合起來看做 Advantage function $A^{\theta}(s_t,a_t)$
    • 這邊 Reward 不管你是什麼形式，有沒有 discount。
    • 它的意義是，這個 action 相較於其他的 action 有多好，而不是絕對好
  • 這個 A 通常可以由某個類神經網路估計，那個類神經網路叫做 critic，以後講 Actor-Critic 的時候再說