paper: Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
Abstract
本文提出一個新的 vision Transformer,稱作 Swin Transformer,可以被用作 computer vision 中的 general-purpose backbone。
把 Transformer 從 language 移到 vision 具備挑戰性,比如同一個 visual entity 在大小上具備很大的 variance。還有 high resolution 下 pixel 和 word 的數量差異太大。
為了解決這些差異,作者提出 hierachical Transformer,用 shifted windows 來算出 representation。
shifted windowing 透過把 self-attention 限制在 non-overlapping 的 local window 和允許 cross-windows connection 來提高效率。
這種 hierarchical architecture 可以靈活地在各種 scale 下擴展 model,還可以對圖像大小有線性的計算時間複雜度。
Introduction
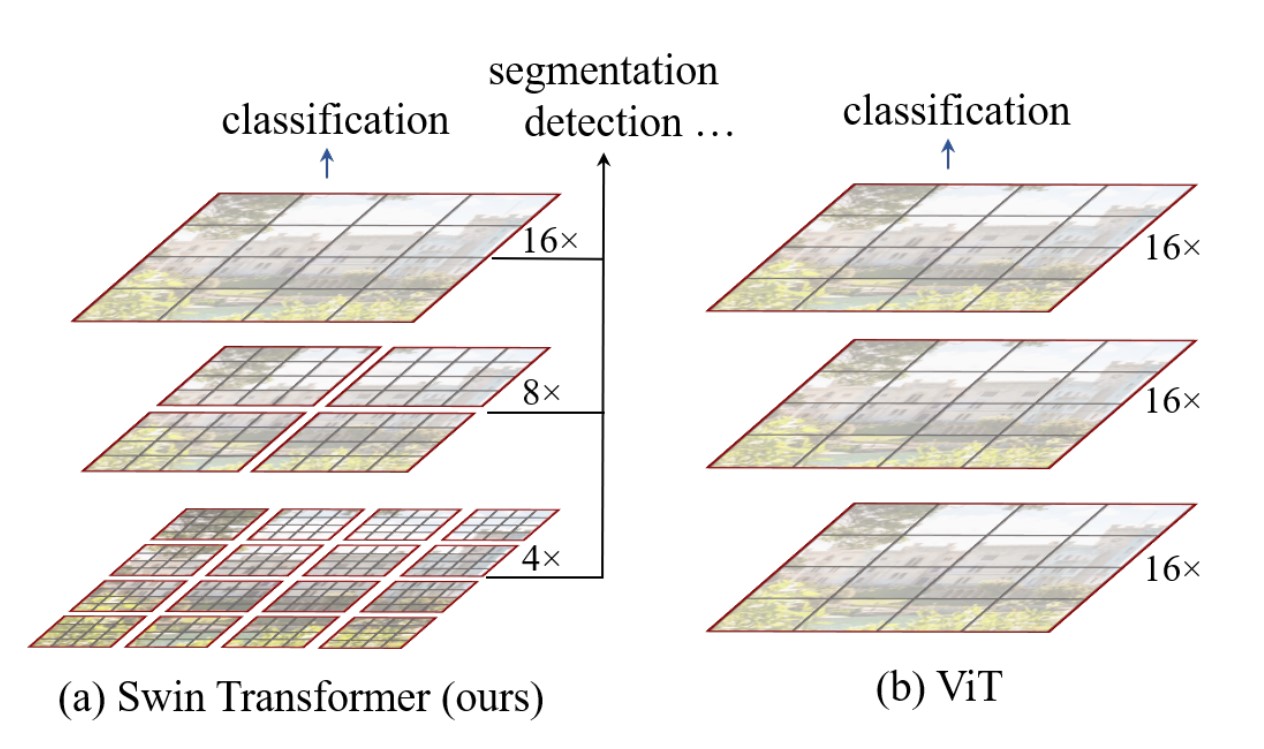
ViT 把圖片打成 patch,每個 patch 是 16*16,feature maps 由 single low resolution 的輸入生成,而且由於自注意力始終都是在全局上計算的 (patch 和 patch 間做自注意力),所以時間複雜度是 quadratic computation complexity。
Swin Transformer 從小 patch 開始,並在更深的 Transformer layers 合併相鄰的 patches。
有了這些 hierarchical feature maps,可以用在像是 FPN 或是 U-Net。
一個 Swin Transformer 的關鍵設計因素是 shifted window。
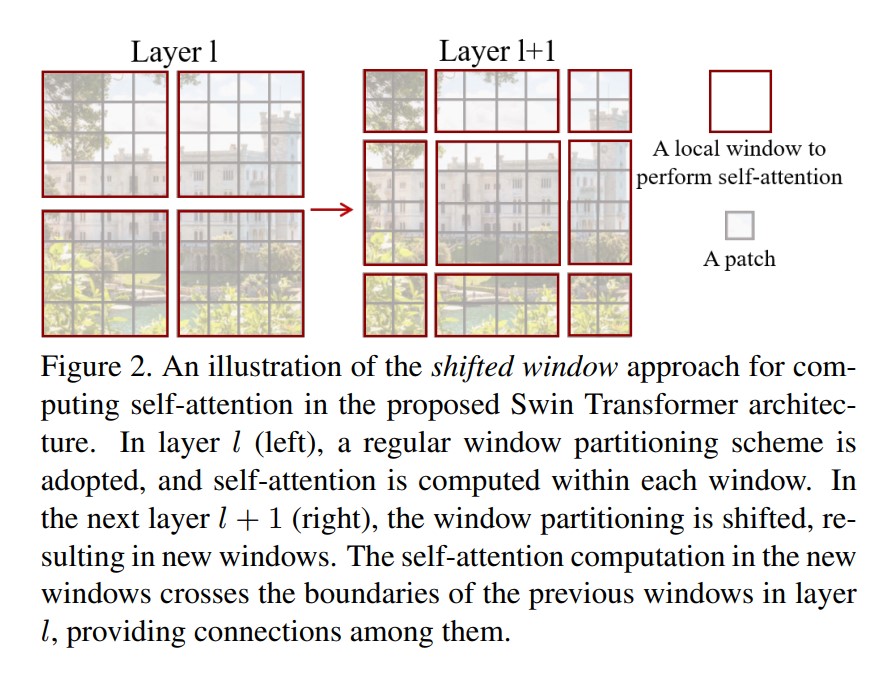
透過 bridge 不同 layer 的 windows 來提供他們連接。
Method
Overall Architecture
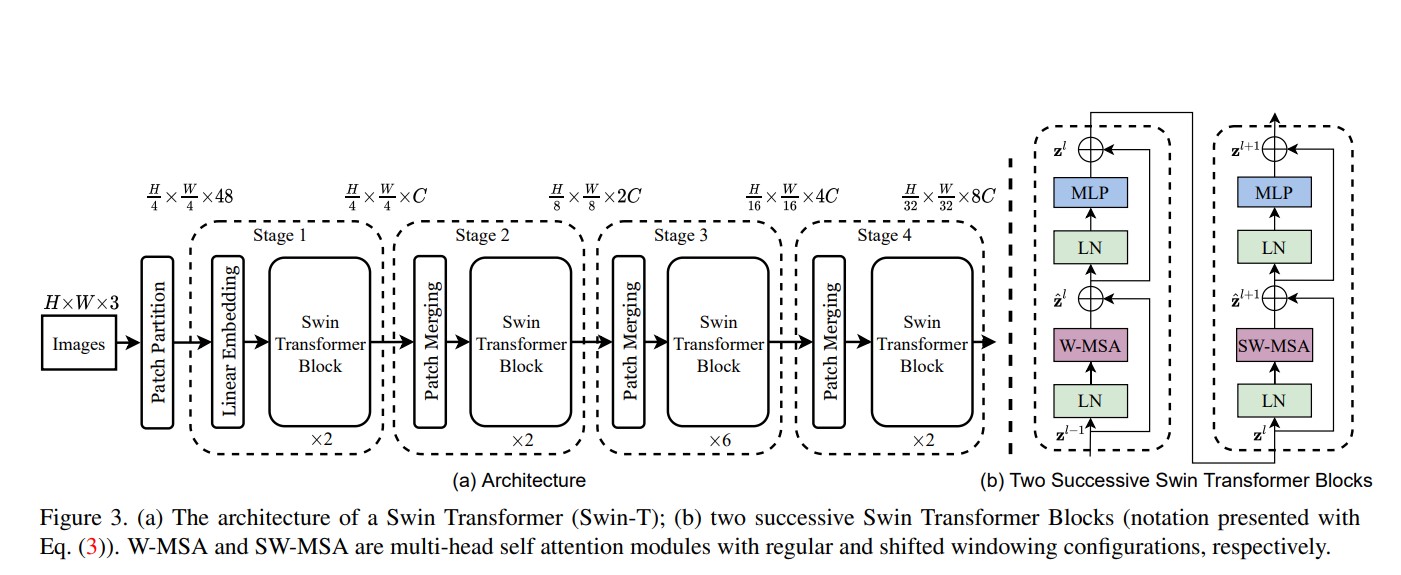
- Patch Merging
- 原本特徵圖是 H * W * C
- 以上下 stride=2 行走,會得到四張 H/2 * W/2 * C
- concatenate 起來,變成 H/2 * W/2 * 4C
- 做 linear,變成 H/2 * W/2 * 2C
Swin Transformer block
Swin Transformer 是透過把 Transformer block 中的 multi-head self attention(MSA) 換成基於 shifted windows 的 module 構成。
Shifted Window based Self-Attention
標準的 Transformer 架構會算 global self-attention,計算所有 token 間彼此的關係,導致 quadratic complexity,使其不適用於需要大量 token 的許多 CV 問題
Self-attention in non-overlapped windows
原來的圖片會以 non-overlapping 的方式切割。
假設每個 windows 有 M * M 個 patches,然後一張圖像有 h * w 塊 patches,計算複雜度如下:
- $\Omega(MSA)=4hwC^2+2(hw)^2C$
- $\Omega(W-MSA)=4hwC^2+2M^2hwC$
Shifted window partitioning in successive blocks
window-based self-attention module 缺乏了 windows 間彼此的連接,會限制模型能力。
作者提出了一種 shifted window 的方法,保持 non-overlapping windows 的高效計算,同時引入 windows 間的連接。
再兩個連續的 windows 間,會移動 $(⌊ \frac{M}{2} ⌋, ⌊ \frac{M}{2} ⌋)$
Efficient batch computation for shifted configuration
shifted window 有個問題是,會導致更多的 windows,從 $⌈ \frac{h}{M} ⌉ * ⌈ \frac{w}{M} ⌉$ 到 $(⌈ \frac{h}{M} ⌉+1) * (⌈ \frac{w}{M} ⌉+1)$,而且有些 window 會小於 M*M。
這樣會導致無法把這些給壓成一個 batch 快速計算。
一種 naive 的解法就是直接在外面加 zero padding,但會增加計算量,當 windows 數量較少時,計算量會變很可觀 (從 2 * 2 個 windows 變成 3 * 3 個 windows,增加了 2.25 倍)
作者提出另外一種巧妙的做法,把一些部分挪移。
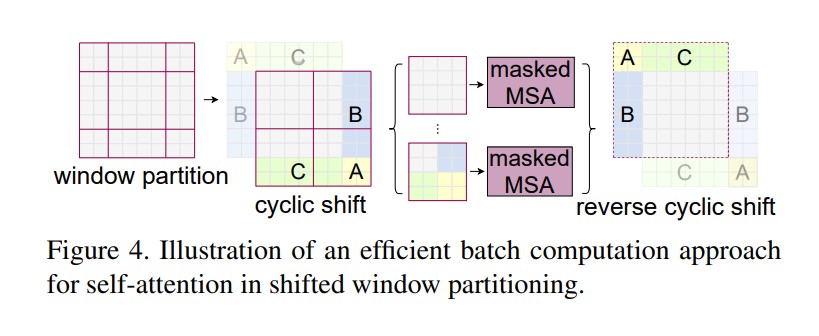
但現在有些 window 裡有多個不該相互做 attention 的部分,所以要用 mask 的方式計算。
不同 windows,做 self-attention 後,把不相干的部分做的 attention 減去一個很大的數值,最後再過 softmax。
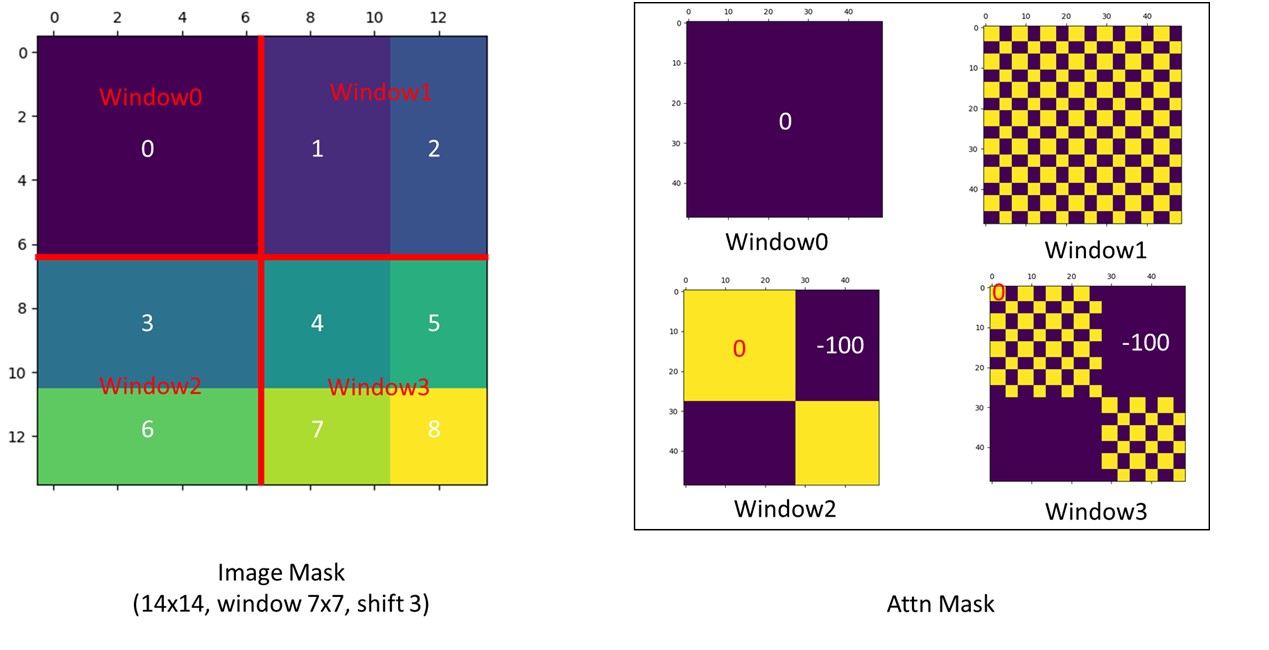
上圖來自作者在 github 提供的可視化
最後再把它挪回原本的位置。
Relative position bias
參考這個: https://blog.csdn.net/qq_37541097/article/details/121119988
Architecture Variants
-
window size 預設是 M = 7
-
query dimension of each head 是 d = 32
-
expansion layer of each MLP is $\alpha$ = 4
-
C 是 first stage 的 hidden layers 的 channel numbers
-
Swin-T
- C = 96
- layer numbers = {2, 2, 6, 2}
- 大小和計算量是 Base 的大約 0.25 倍
- complexity 接近 ResNet-50
-
Swin-S
- C = 96
- layer numbers = {2, 2, 18, 2}
- 大小和計算量是 Base 的大約 0.5 倍
- complexity 接近 ResNet-101
-
Swin-B
- C = 128
- layer numbers = {2, 2, 18, 2}
-
Swin-L
- C = 192
- layer numbers = {2, 2, 18, 2}
- 大小和計算量是 Base 的大約 2 倍
Experiments
Image Classification on ImageNet-1K
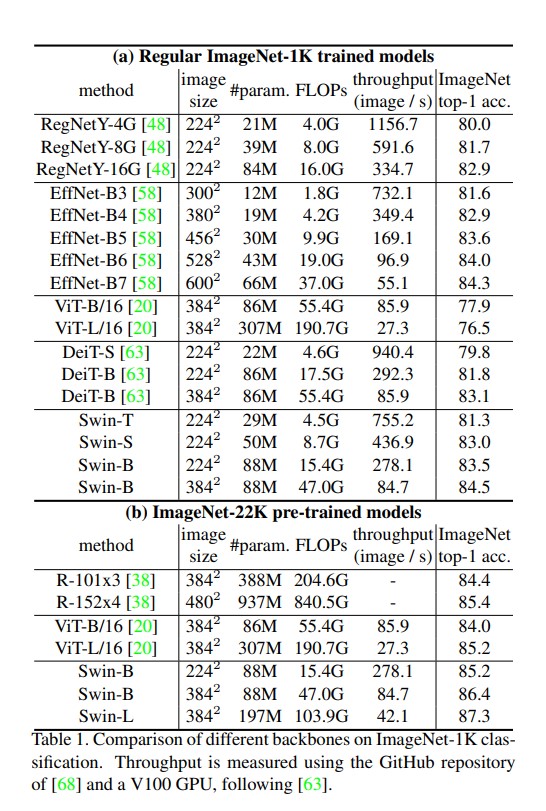
Object Detection on COCO
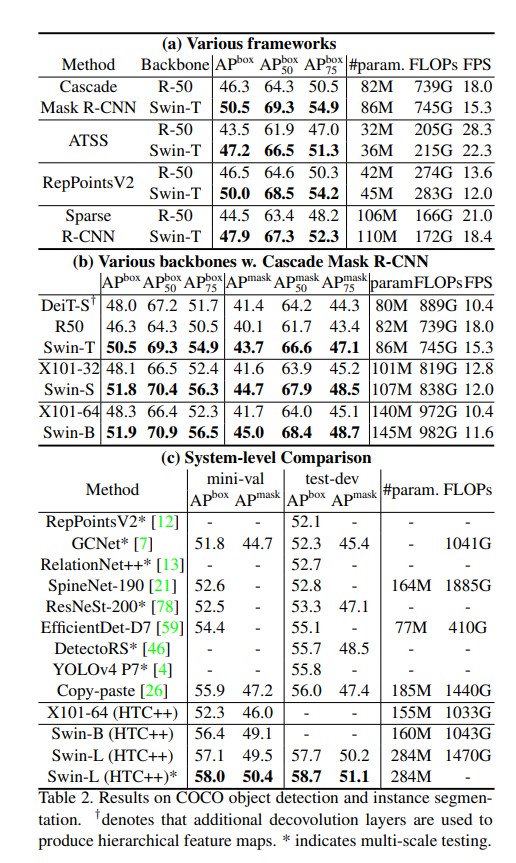
Semantic Segmentation on ADE20K
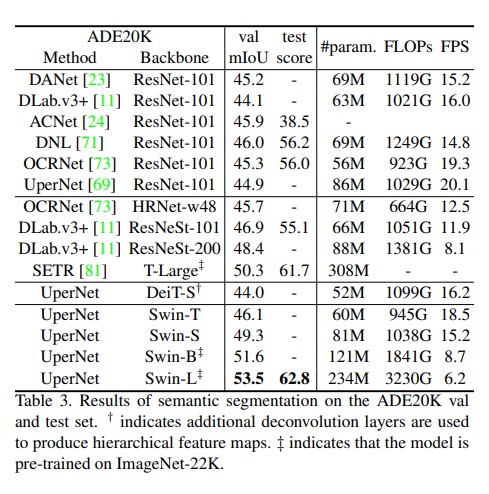
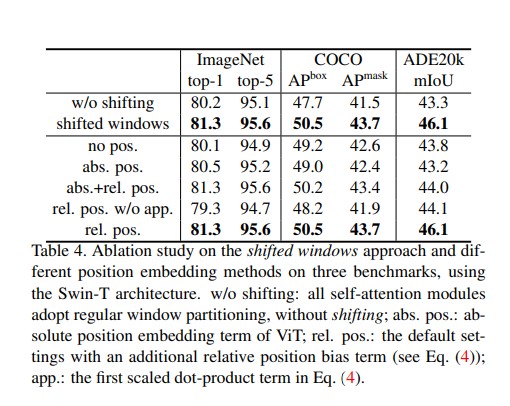
Ablation Study
Conclusion
基於 self-attention 的 shifted window 是 Swin Transformer 關鍵部分,被顯示出他在 CV 領域有效率且有效,並期望未來把它應用在 NLP。