說明
本文寫於 Swin Transformer 論文閱讀 之後,當時對 Relatvie position 的理解不夠清楚,本文將會做解釋,並附上原論文的筆記。
以下將會先用長度為 3 的序列作為示範。
Absolute Position Encodings
Absolute Position Encodings 的做法是把用某種方式生成或可學習的向量加在輸入,第一個位置用 $w_1$,第二個位置用 $w_2$,第三個位置用 $w_3$。
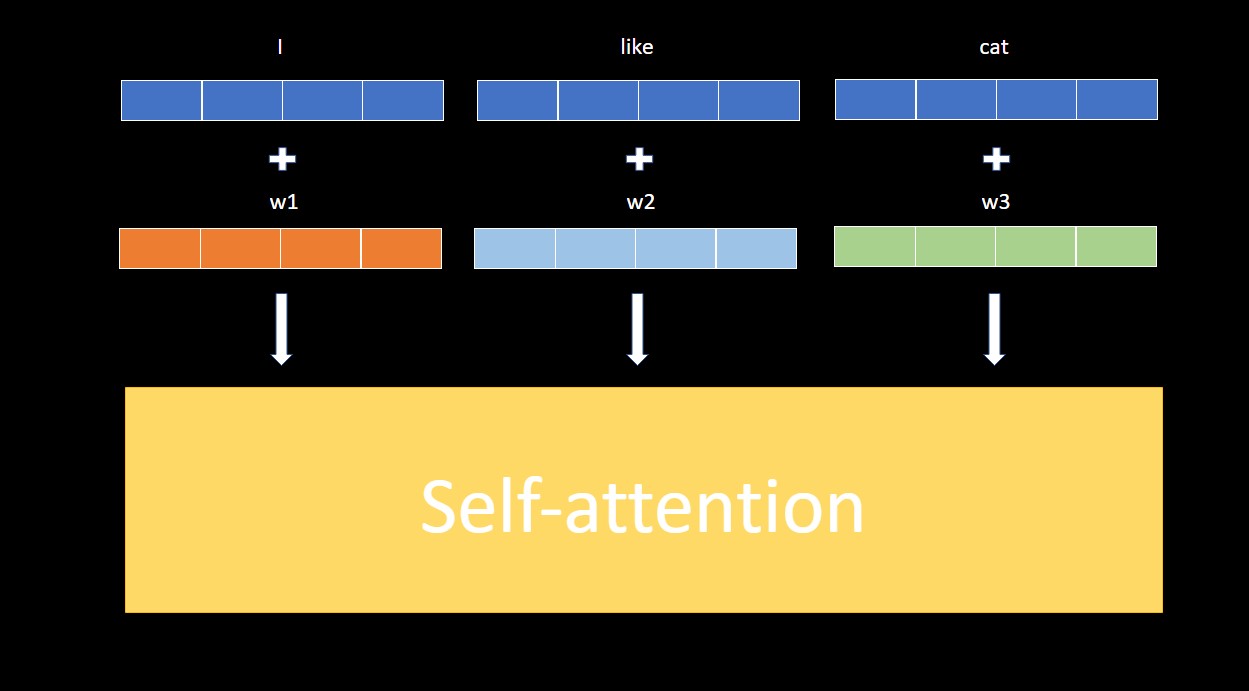
Relative Position Encodings
Relative Position Encodings 顧名思義,就是改用相對位置來做這些向量。
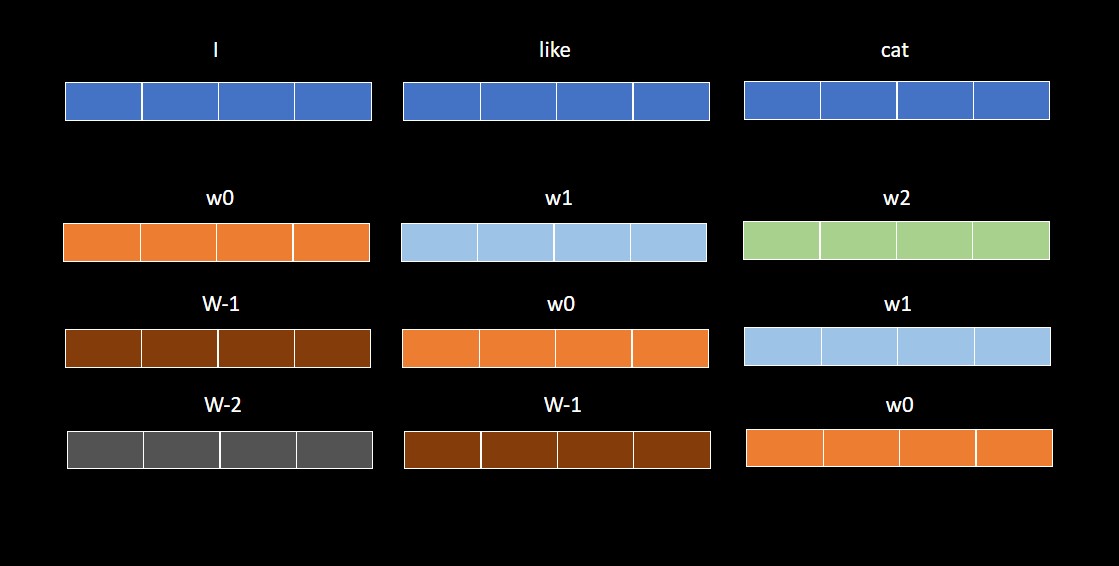
上圖中,Position Encoding 的部分從 3 個向量變成 3*3 個向量,因為現在會以每個 token 為基準,生出 3 個相對位置向量。
我們以 $w_0$,代表處於原點,$w_x$ 代表往右 $x$ 格,$w_{-x}$ 代表往左 $x$ 格,其中 $x$ 是正整數。
第一個 row 有 $w_0$、$w_1$、$w_2$,意思是以第 0 個向量 (I) 為基準,他的位置是 $w_0$,對第 0 個向量來說,第 1 個向量 (like) 是 $w_1$,第 2 個向量 (cat) 是 $w_2$。
輪流以 $n$ 個 token 為基準,就會生出 n*n 個相對位置向量,而不是原先的 n 個絕對位置向量。
其中 $w_i$ 和 $w_j$ 如果 $i=j$,他們會共用同樣的 weight,上圖是以相同顏色表示。
如果序列長度是 $n$,就會有 $2n-1$ 個向量要學。
n*n 這個數量使其適合加入到 self-attention,原始論文的加入方式可以參考下方論文筆記,這邊晚點會介紹後續衍生的簡化版。
Swin Transformer 如何導入 Relative Position Encodings
Swin Transformer 是借鑒許多 CNN 架構,為了 CV 而經過修改的 vision transformer。
其中一個重點是,他會在一小區塊的特徵圖上做 self-attention,而且是用 Relative Position Encodings。
和剛剛的差別在於,現在要在二維空間做 Relative Position Encodings。

假設有一張 2*2 的 feature map,我們先設定好 feature map 各個 token 的絕對位置座標。
然後我們輪流把 feature map 的每一個 token 作為基準點,把 feature map 的每個 token 的座標減去基準點的座標,就可以得到相對位置座標。
如果我們把四個相對位置座標各別攤平 (按照左上 -> 右上 -> 左下 -> 右下的順序),並且從上到下排好,他會看起來如下圖。
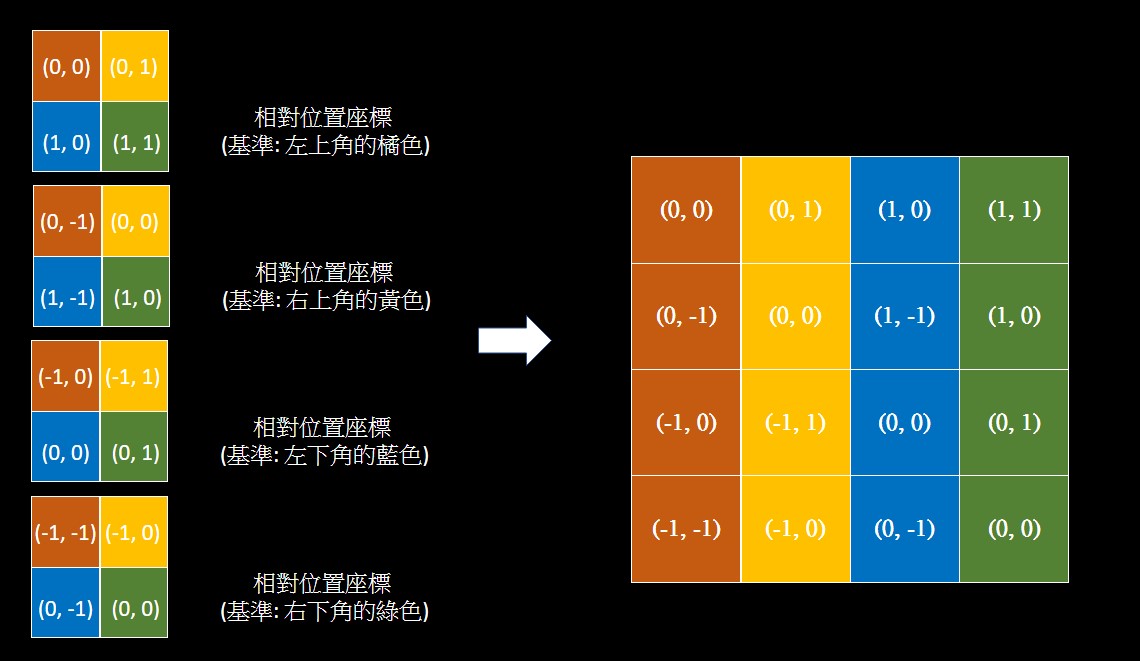
此時我們幾乎完成了相對位置的表,和剛剛序列一樣生出了 n*n 個相對位置。
我們接下來要做的事情是把這個表給編號,把 (0, 0) 都編成某個數字,把 (1, 0) 都編成某個數字。
在此之前,先考慮總共會有幾種可能的相對座標,對於邊長 $M$ 的 feature map (這裡 M=2),因為兩軸可能的數字皆有 (2M-1) 種,共會有 (2M-1)*(2M-1) 種可能性,這裡等於 9。
所以我們等等會把所有座標編為 0~8。
想從座標生出編號 0~8 可以考慮把座標兩軸的數字相加,但由於有負數的存在,要先把兩軸的數字都變成非負整數,所以先把兩軸的座標都各別加 M-1。

此時如果相加,會使 (2, 1) 和 (1, 2) 都對應到數字 3,所以我們先把 row 座標乘上 2M-1 再相加,此時就可以獲得一個 n*n 的 index table ,對應一組相對位置向量。
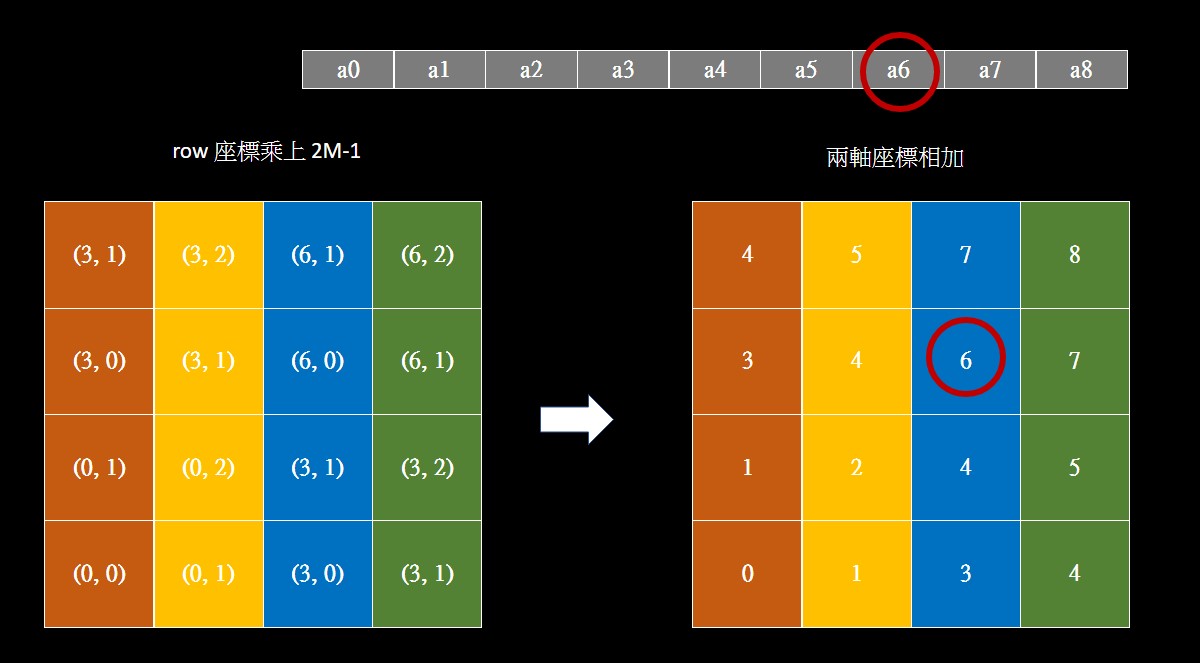
Swin Transformer 是用簡化版的作法來引入相對位置,公式如下
- $Attention(Q,K,V)=SoftMax(QK^T/\sqrt{d}+B)V$
- $B$ 是 relative position bias,$B \in R^{M^2 * M^2}$
- $a_{ij}$ 是純量,不是向量,和原始論文不同
論文出處
paper: Self-Attention with Relative Position Representations
Abstract
依賴於 attention 機制的 Transformer 在機器翻譯方面取得 SOTA,但在結構中沒有相對或絕對的位置資訊,他需要在輸入中添加絕對位置的資訊。
因此本文提出一種替代方案,拓展 self-attention ,考慮相對位置的表示,並在一些任務中獲得更好的結果。
值得一題的事,作者觀察到結合相對和絕對位置不會進一步提高翻譯品質。
該機制可以拓展到任意 graph-labeled 的輸入
Introduction
Non-recurrent models 不一定按順序考慮輸入元素,因此可能需要明確的 position encoding 才才能用序列順序。
一種常見的方法是使用與輸入元素結合的 position encoding,以向模型傳達位置資訊。
可以是 deterministic function,或是 learned representations。
CNN 可以捕捉 kernel 的相對位置資訊,但被證明仍受益於 position encoding。
對於既不使用卷積也不使用遞歸的 Transformer,結合位置信息的 representation 是一個特別重要的考慮因素,因為該模型在其他方面對序列排序完全不變。
本文提出一種將相對位置合併到 Transformer 的 self-attention 的做法,即使完全換掉絕對位置編碼,也使兩個機器翻譯任務的品質有顯著提高。
Background
-
原始 self-attention
-
$z_i=\displaystyle\sum_{j=1}^n\alpha_{ij}(x_jW^V)$
-
$\alpha_{ij}=\frac{\text{exp } e_{ij}}{\sum_{k=1}^n\text{exp } e_{ik}}$
-
$e_{ij}=\frac{(x_iW^Q)(x_jW^K)^T}{\sqrt{d_z}}$
Proposed Architecture
Relation-aware Self-Attention
有兩個要引入 relative position 的地方,而且都是向量
-
$z_i = \displaystyle\sum_{j=1}^n \alpha_{ij}(x_jW^V+a_{ij}^V)$
-
$e_{ij}=\frac{x_iW^Q(x_jW^K+a_{ij}^K)^T}{\sqrt{d_z}}$
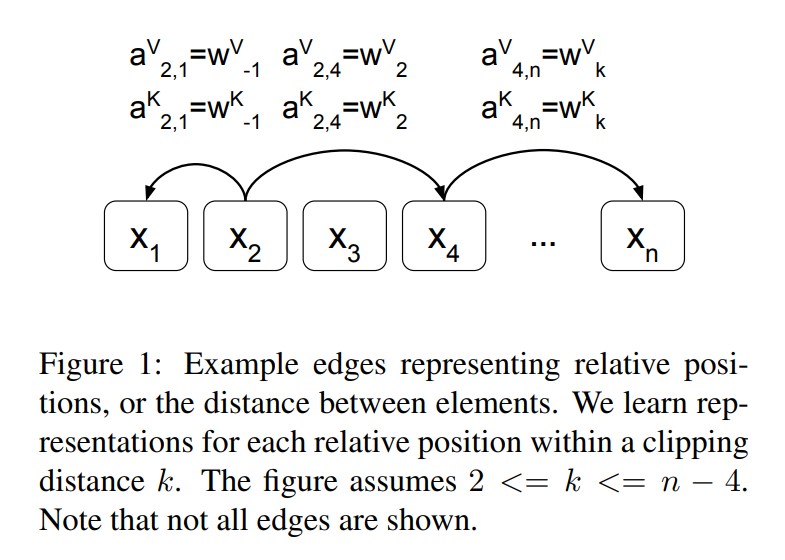
Relative Position Representations
可以引入 clip,把線性序列中,高於長度 k 的修剪成最大值
- $a_{ij}^K=w_{clip(j-i,k)}^K$
- $a_{ij}^V=w_{clip(j-i,k)}^V$
- $clip(x,k)=max(-k,min(k,x))$
Experiments
Model Variations
-
clipping 的實驗

-
V 和 K 的 ablation study
