RL 方法
- Policy-based
- learn 做事的 actor
- Value-based
- 不直接 learn policy,而是 Learn critic,負責批評
- Q-learning 屬於這種
Critic
- 不直接決定 action
- 給予 actor $\pi$,評估 actor $\pi$ 有多好
- critic 的 output 依賴於 actor 的表現
State Value Function
- State value function $V^{\pi}(s)$
- 用 actor $\pi$,看到 s 後玩到結束,cumulated reward expectation 是多少
評估方法
-
Monte-Carlo(MC) based approach
- critic 看 $\pi$ 玩遊戲
- 訓練一個 network,看到不同的 state ,輸出 cumulated reward(直到遊戲結束,以下稱為 $G_a$),解 regression 問題
-
Temporal-difference(TD) approach
- MC 的方法至少要玩到遊戲結束才可以 update network,但有些遊戲超長
- TD 只需要 {$s_t,a_t,r_t,s_{t+1}$}
- $V^{\pi}(s_t)=V^{\pi}(s_{t+1})+r_t$
- MC 的方法至少要玩到遊戲結束才可以 update network,但有些遊戲超長
-
MS v.s. TD
- MC
- Larger variance
- 每次的輸出差異很大
- Larger variance
- TD
- smaller variance
- 相較 $G_a$ 較小,因為這邊的 random variable 是 r,但 $G_a$ 是由很多 r 組合而成
- V 可能估得不準確
- 那 learn 出來的結果自然也不准
- 較常見
- smaller variance
- MC
Another Critic
-
State-action value function $Q^\pi(s,a)$
- 又叫 Q function
- 當用 actor $\pi$ 時,在 state s 採取 a 這個 action 後的 cumulated reward expectation
- 有一個要注意的地方是,actor 看到 s 不一定會採取 a
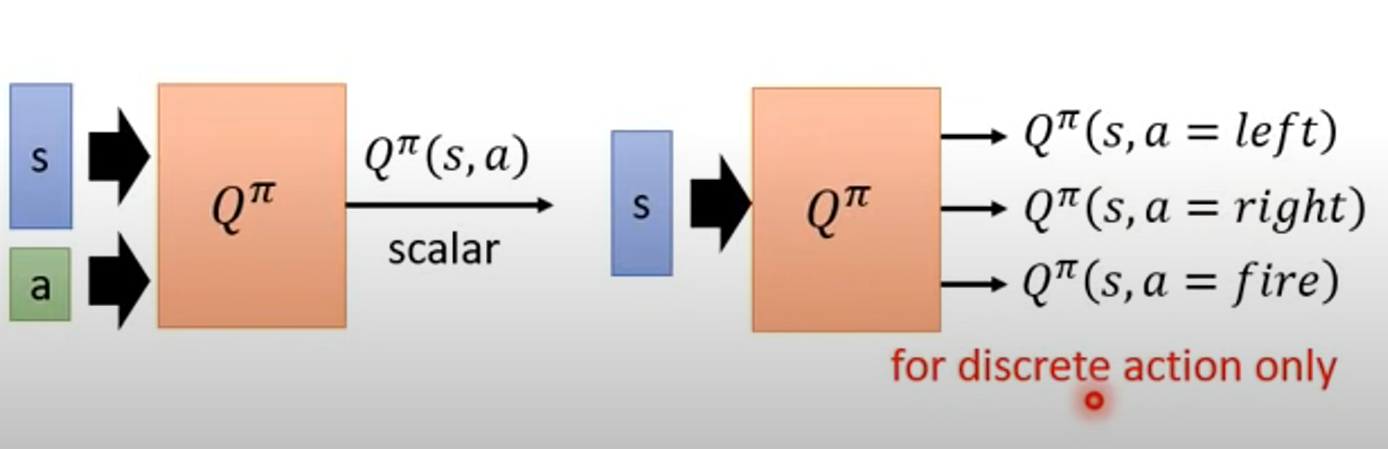
- 只要有 Q function,就可以找到"更好的" policy,再替換掉原本的 policy
- “更好的"定義
- $V^{\pi^{’}} \ge V^{\pi}(s), \text{for all state s}$
- $\pi^{’}(s)=arg \underset{a}{max}Q^{\pi}(s,a)$
- $\pi^{’}$ 沒有多餘的參數,就單純靠 Q function 推出來
- 這邊如果 a 是 continuous 的會有問題,等等解決
- 這樣就可以達到"更好的"policy,不過就不列證明了
- “更好的"定義
Basic Tip
Target network
- 在 training 的時候,把其中一個 Q 固定住,不然要學的 target 是不固定的,會不好 train
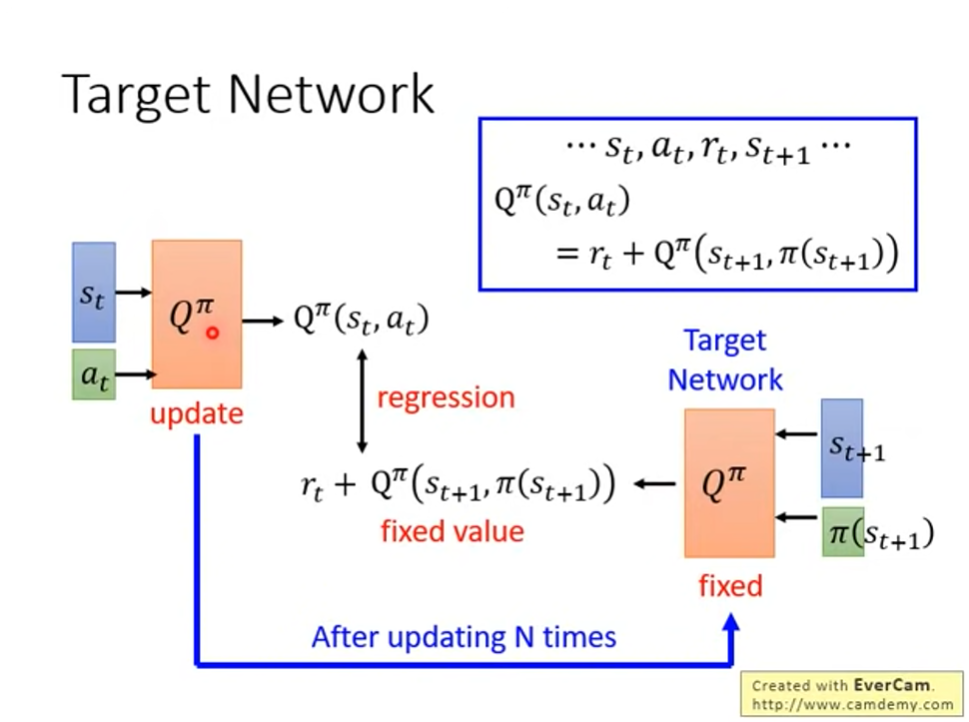
Exploration
- policy 完全 depend on Q function
- 如果 action 總是固定,這不是好的 data collection 方法,要在 s 採取 a 過,才比較好估計 Q(s, a),如果 Q function 是 table 就根本不可能估出來,network 也會有一樣的問題,只是沒那麼嚴重。
解法
- Epsilon Greedy
- $a=\begin{cases} arg \underset{a}{max}Q(s,a), & \text{with probability } 1-\varepsilon \\ random, & otherwise \end{cases}$
- 通常 $\varepsilon$ 會隨時間遞減,因為你一開始 train 的時候不知道怎麼比較好
- Boltzmann Exploration
- $P(a|s)=\frac{exp(Q(s,a))}{\sum_a exp(Q(s,a))}$
Replay Buffer
- 把一堆的 {$s_t,a_t,r_t,s_{t+1}$} 存放在一個 buffer
- {$s_t,a_t,r_t,s_{t+1}$} 簡稱為 exp
- 裡面的 exp 可能來自於不同的 policy
- 在 buffer 裝滿的時候才把舊的資料丟掉
- 每次從 buffer 隨機挑一個 batch 出來,update Q function
好處
- 跟環境作互動很花時間,這樣可以減少跟環境作互動的次數
- 本來就希望 batch 裡的 data 越 diverse 越好,不會希望 batch 裡的 data 都是同性質的
issue
- 我們要觀察 $\pi$ 的 value,混雜了一些不是 $\pi$ 的 exp 到底有沒有關係?
- 理論上沒問題,但李老師沒解釋
Typical Q-learning 演算法
- 初始化 Q-fucntion Q,target Q-function $\hat{Q}=Q$
- 在每個 episode
- 對於每個 time step t
- 給 state $s_t$,根據 Q 執行 action $a_t$ (epsilon greedy)
- 獲得 reward $r_t$,到達 $s_{t+1}$
- 把 {$s_t,a_t,r_t,s_{t+1}$} 存到 buffer
- 從 buffer sample {$s_t,a_t,r_t,s_{t+1}$}(通常是一個 batch)
- Target $y=r_i+\underset{a}{max}\hat{Q}(s_{i+1},a)$
- Update Q 的參數,好讓 $Q(s_i,a_i)$ 更接近 y(regression)
- 每 C 步 reset $\hat{Q}=Q$
- 對於每個 time step t
Adveanced Tip
Double DQN
- Q Value 往往被高估
- 我們的目的是要讓 $Q(s_t, a_t)$ 和 $r_t+\underset{a}{max}Q(s_{t+1},a)$ 越接近越好(後者就是 target)
- target 常常不小心設太高,因為如果有 action 被高估了,就會選那個當 target
- Double DQN: 兩個函式 $Q$ 和 $Q^{’}$
- 把 target 換成 $r_t+Q^{’}(s_{t+1},arg \underset{a}{max}Q(s_{t+1},a))$
- 選 action 交給 $Q$,實際算交給 $Q^{’}$
- 如果 $Q$ 選了高估的 action,$Q^{’}$ 有可能修正回來
- 如果 $Q^{’}$ 高估,$Q$ 不一定會選到
- $Q^{’}$ 是 target network(固定不動)
Dueling DQN
- 改變 network 架構
- 分成兩條 path
- 第一條算 scalar
- 第二條算 vector,每個 action 都有個 value
- 把 scalar 加到每一個維度
- 只更改到 V(s) 的時候,會全部的 action 都改到,可能會是一個比較有效率的方式,不用 sample 所有的 action
- 但有可能模型不管 V(s),直接設 0,只改 A
- 所以會對 A 下 constrain,讓 network 傾向於改 V
- 比如同個 state 下的所有 action 要生出 A(s,a) 總和為 0
- 在 A 的輸出加個 normalization 即可辦到,這個 normalization 就是把每個維度都減掉平均
- 比如同個 state 下的所有 action 要生出 A(s,a) 總和為 0
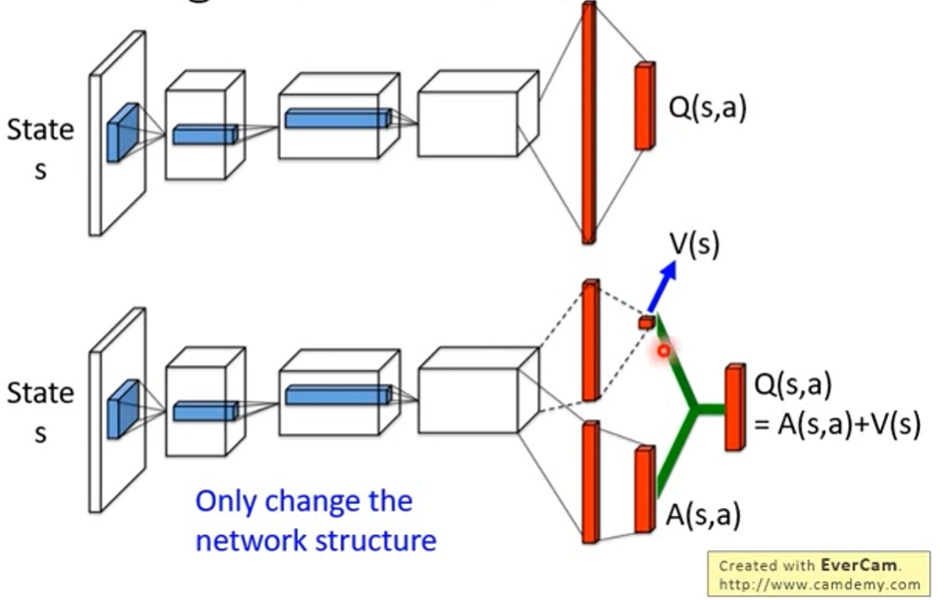
Prioritized Replay
- 原本是 uniform 的從 buffer sample data
- 改讓 「有更大的 TD error」的 data 有更高的機率被 sample
- TD error 就是 $Q(s_t, a_t)$ 和 target 的差距
- 實際在做的時候有額外的細節,不會只改 sampling 的 process,還要改 update 參數的方法
Multi-step
- Balance between MC 和 TD
- TD 只需要存 {$s_t,a_t,r_t,s_{t+1}$}
- 改存 {$s_t,a_t,r_t,…,s_{t+N},a_{t+N},r_{t+N}, s_{t+N+1}$}
- 我們的目的是要讓 $Q(s_t, a_t)$ 和 $\displaystyle\sum_{t^{’}=t}^{t+N} r_{t^{’}}+\hat{Q}(s_{t+N+1},a_{t+N+1})$ 越接近越好(後者就是 target)
- $a_{t+N+1}=arg\underset{a}{max}\hat{Q}(s_{t+N+1},a)$
- 同時有 MC 和 TD 的好處和壞處
- 估測的影響比較輕微
- r 比較多項,variance 比較大
Noisy Net
- improve exploration
- Noise on Action
- Epsilon Greedy(之前的回顧)
- $f_X(x) = \begin{cases} arg \underset{a}{max}Q(s,a), & \text{with probability }1-\varepsilon \\ random, & ,otherwise \end{cases}$
- 給同樣的 state,採取的 action 不一定一樣
- 沒有真實的 policy 會這樣運作
- Epsilon Greedy(之前的回顧)
- Noise on Parameters
-
$a = arg \underset{a}{max}\tilde{Q}(s,a)$
- 在每個 episode 剛開始的時候,在 Q-function 的參數上面加上 gaussian noise
-
給同樣的 state,採取同樣的 action
- 叫做 state-dependent exploration
-
explore in a consistent way
-
Distributional Q-function
- Q-function 生出的東西是 cumulated reward 的期望值
- 所以我們是在對 distribution 取 mean,但不同的 distribution 也可能有同樣的 mean
- 想做的事情是 model distribution
- 如果有做這個,就比較不會有 over estimate reward 的結果,反而容易 under estimate,使 double 比較沒用
- output 的 range 不可能無限寬,超過邊界的 reward 會被丟掉
Rainbow
- 綜合一堆方法
Continuous actions
- Q learning 不容易處理 continuous action
Solution
-
sample n 個可能的 a,都丟 Q function 看誰最大
-
gradient descent
- 把 a 當作 parameter,要找一組 a 去 maximize Q function
- 運算量大,要 iterative 的 update a
- 不一定可以找到 global 的最佳解
- 把 a 當作 parameter,要找一組 a 去 maximize Q function
-
特別設計 Q network,讓解 optimization 的問題變容易
- 範例
- Q network 輸出 $\mu(s)$、$\Sigma(s)$、$V(s)$,個別是 vector、matrix、scalar
- a 是 continuous 的 Action,是一個 vector,每個維度都是實數
- $\Sigma(s)$ 是 positive definite 的,實作的時候會把 $\Sigma$ 和它的 transpose 相乘
- $Q(s,a)=-(a-\mu(s))^T\Sigma(s)(a-\mu(s))+V(s)$
- $(a-\mu(s))^T\Sigma(s)(a-\mu(s))$ 這項必為正,所以 $a=\mu(s)$ 的時候就是最佳解
- 範例
-
不要用 Q-learning