paper: Memorizing Normality to Detect Anomaly: Memory-augmented Deep Autoencoder for Unsupervised Anomaly Detection

Abstract

autoencoder 在收到異常輸入的時，預期會生出較高的 reconstruction error。但是這個假設實際上並不總是發生。他有可能「泛化」的很好，導致異常的也可以正常重建。

為了緩解這個問題，本文幫 auto-encoder 加上一個 memory 的機制。

訓練階段，memory 要學習生成 normal data 的 prototypical elements。

測試階段，learned memory 會被固定住，然後要根據 few selected memory 進行重建。

對於異常輸入，這個重建出的東西就會比較像是 normal sample。這樣 reconstruction error 就會被增強。

MemAE 是 free of assumption，所以可以用在各種不同的任務上。

Introduction

AE 有可能「泛化」的很好，導致對於異常輸入也可以正常重建。如果 anomolies 和 normal pattern 有共享某些 composition pattern，或是 decoder 強到連 abnormal encoding 都可以重建，就可能發生這樣的狀況。

MemAE 多了一個 memory module，從 encoder 出來的東西會被視作 query，用來把 memory 中最相關的元素取出，然後作 aggregation。

作者還進一步提出了一個不同的 hard shrinkage operator，可以生出 sparsity of memory addressing weight。

在訓練階段，會把 memory content 連同 encoder 和 decoder 一起訓練，透過 sparse addressing strategy，MemAE 可以有效地利用有限的 memory slot 來製造出 prototypical normal patterns，來製造出夠低的 reconstruction error。

在測試階段，memory content 會被固定住，然後根據 few selected memory 來重建。因為 memory module 並不是基於某種特定資料的假設，所以可以用在各種不同的任務上。

Memory-augmented Autoencoder

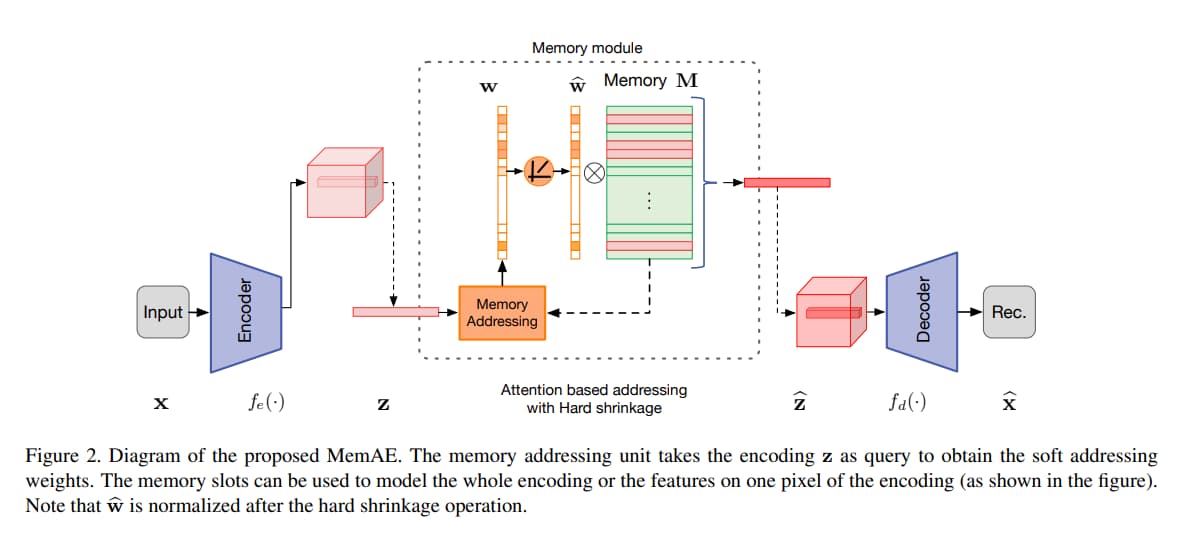
Memory Module with Attention-based Sparse Addressing

Attention for Memory Addressing

• attention weight $w_i$
  • $w_i=\frac{exp(d(z,m_i))}{\sum^{N}_{j=1}exp(d(z,m_j))}$
  • $d(\cdot, \cdot)$ 是 similarity measurement，這裡是 cosine similarity
    • $d(z,m_i)=\frac{zm_i^T}{||z|| \text{ } ||m_i||}$

Hard Shrinkage for Sparse Addressing

• hard shrinkage
  • $\hat{w}_i=h(w_i;\lambda)=\begin{cases} w_i & \text{if } w_i>\lambda \\ 0 & \text{otherwise} \end{cases}$
    • 這東西不好做 backpropagation
  • 改良版
    • $\hat{w}_i=\frac{max(w_i-\lambda,0)}{|w_i-\lambda|+\epsilon}$
      • $max(\cdot, 0)$ 就是 ReLU
      • 根據實驗，把 $\lambda$ 設在 [1/N, 3/N] 會得到還不錯的結果
  • shrinkage 後會再 normalize
    • $\hat{w}_i=\hat{w}_i/||\hat{w}||_1$

Sparse addressing 有助於鼓勵模型用更少但相關的 memory item 來表示 query。

鼓勵 memory addressing 的 sparsity 是有益的，因為 memory M 被訓練來適應 sparse w。

鼓勵 sparsity 也可以緩解異常樣本可以被很好的重建的問題。

Training

• 分成兩個 loss
  • Reconstruction error
    • $R(x^t, \hat{x}^t)=||x^t-\hat{x}^t||^2_2$
      • $l2-norm$
  • entropy of $\hat{w}^t$
    • 用來進一步提升 sparsity
    • $E(\hat{w}^t)=\sum^{T}_{i=1}-\hat{w}_i \cdot log(\hat{w}_i)$
• Combine
  • $L(\theta_e, \theta_d, M)=\frac{1}{T}\sum^{T}_{t=1}(R(x^t, \hat{x}^t)+\alpha E(\hat{w}^t))$
    • 根據實驗，$\alpha$ 設成 0.0002