Introduction
結合 policy-based 和 value-based
- A3C
- Actor-Critic 最知名的方法
- Advantage Actor-Critic 是 A2C
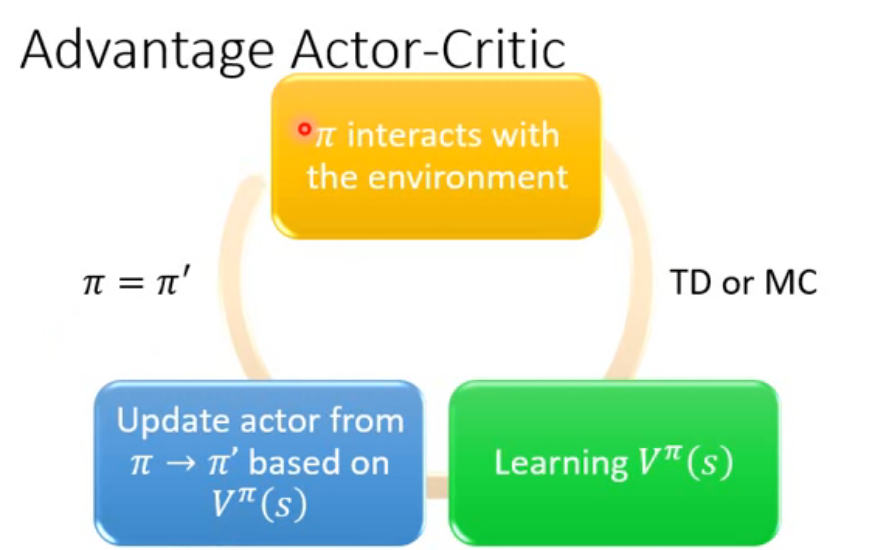
Advantage Actor-Critic
-
Review: Policy gradient
- $\triangledown \overline{R_{\theta}}\approx \frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{t=1}^{T_n}(\displaystyle\sum_{t^{’}=t}^{T_n}\gamma^{t^{’}-t}r_{t^{’}}^n-b)\triangledown log p_{\theta}(a_t^n|s_t^n)$
- $G_t^n=\displaystyle\sum_{t^{’}=t}^{T_n}\gamma^{t^{’}-t}r_{t^{’}}^n-b$
- G very unstable,因為給同樣的 state 作同樣的 action 不一定會得到同樣的結果,G 是個 random variable
- $G_t^n=\displaystyle\sum_{t^{’}=t}^{T_n}\gamma^{t^{’}-t}r_{t^{’}}^n-b$
- $\triangledown \overline{R_{\theta}}\approx \frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{t=1}^{T_n}(\displaystyle\sum_{t^{’}=t}^{T_n}\gamma^{t^{’}-t}r_{t^{’}}^n-b)\triangledown log p_{\theta}(a_t^n|s_t^n)$
-
想要改獲得期望值,取代掉 sample 的值(G 的部分),可以用 Q-Learning
- $E[G_t^n]=Q^{\pi_\theta}(s_t^n,a_t^n)$
- Q function 這樣定義
- 所以我們可以把 G 的部分改用 Q 替換掉,就可以把 Actor 和 Critic 結合起來
- baseline 的部分也可以用 value function 替換掉
- $E[G_t^n]=Q^{\pi_\theta}(s_t^n,a_t^n)$
-
但用 $Q^{\pi}(s_t^n,a_t^n)-V^{\pi}(s_t^n)$ 要一次 estimate 兩個 network
- 可以把 Q 以 V 來表示,那只需要估測 V
- $Q^{\pi}(s_t^n,a_t^n)=E[r_t^n+V^{\pi}(s_{t+1}^n)]$
- 雖然有隨機性(獲得的 reward 和跳到什麼 state 不一定),但先不管期望值 $Q^{\pi}(s_t^n,a_t^n)=r_t^n+V^{\pi}(s_{t+1}^n)$
- 現在雖然多個一個 r,有一些 variance,但也比 G 好
- 可以把 Q 以 V 來表示,那只需要估測 V
$\triangledown \overline{R_{\theta}}\approx \frac{1}{N}\displaystyle\sum_{n=1}^{N}\displaystyle\sum_{t=1}^{T_n}(r_t^n+V^{\pi}(s_{t+1}^n)-V^{\pi}(s_t^n))\triangledown log p_{\theta}(a_t^n|s_t^n)$
Tips
-
actor $\pi(s)$ 和 critic $V^{\pi}(s)$ 的權重可以共享
- 前面幾個 layer 可以 share
-
對 $\pi$ 的 output 下 constrain,讓他的 entropy 不要太小,達到 exploration 的效果
Asynchronous Advantage Actor-Critic
- 一開始有個 global network,開一堆 worker,每次工作前,把 global network 的參數 copy 過去
- 個別去和環境作互動,更新的梯度施加在 global network 上
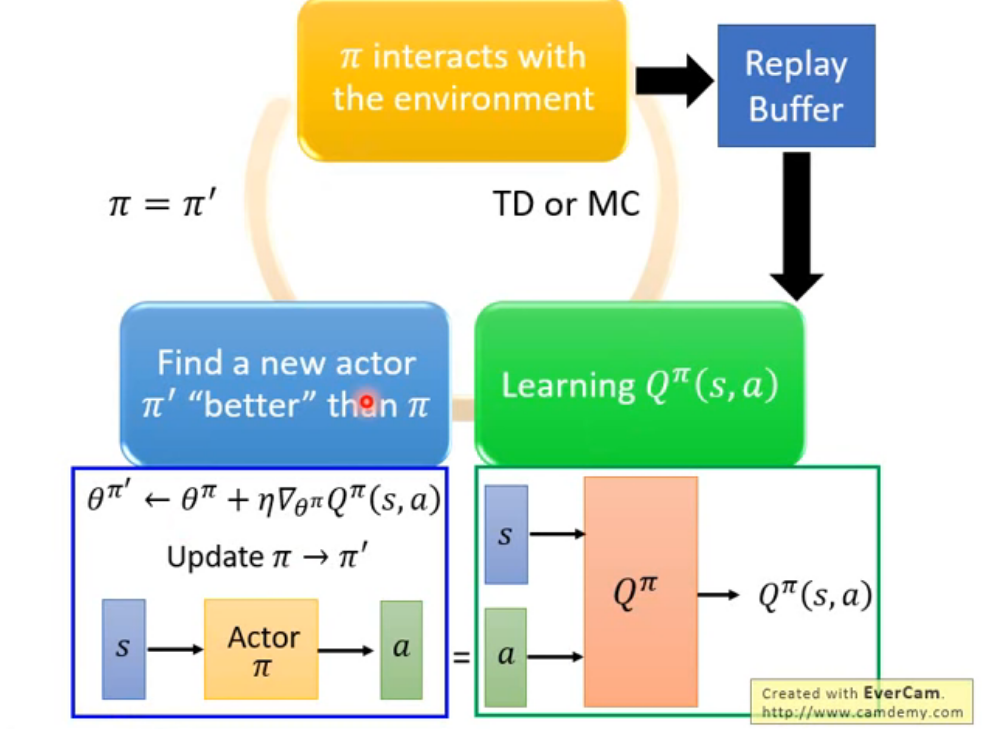
Pathwise Derivative Policy Gradient
- 可以當作是 Q-Learning 解 continuous action 的一種方法
- 訓練一個 actor,目標是生出的 a 餵給 Q 後,可以讓 Q function 的輸出越大越好
- 只會調 actor 的參數,會 fix Q 的
- 就是個 GAN
-
在每個 episode
- 對於每個 time step t
- ⚠️給 state $s_t$,根據 $\pi$ 執行 action $a_t$ (epsilon greedy)⚠️
- 獲得 reward $r_t$,到達 $s_{t+1}$
- 把 {$s_t,a_t,r_t,s_{t+1}$} 存到 buffer
- 從 buffer sample {$s_t,a_t,r_t,s_{t+1}$}(通常是一個 batch)
- ⚠️Target $y=r_i+\hat{Q}(s_{i+1},\hat{\pi}(s_{i+1}))$⚠️
- Update Q 的參數,好讓 $Q(s_i,a_i)$ 更接近 y(regression)
- ⚠️Update $\pi$ 的參數,讓 $Q(s_i,\pi(s_i))$ 最大化⚠️
- 每 C 步 reset $\hat{Q}=Q$
- ⚠️每 C 步 reset $\hat{\pi}=\pi$⚠️
- 對於每個 time step t
-
⚠️ 是和 Q-Learning 不一樣的地方